Calculating interest rates using Newton’s method

by

Here’s a post I wrote for Microfinance Transparency on March 5, 2010

In a previous blog post, I described how to use a spreadsheet like Microsoft Excel to calculate interest rates. Again, interest rate calculations are at the core of MFTransparency’s ability to provide accurate data that can be compared across various products offered by numerous MFIs. In the last post we looked at Excel’s IRR and XIRR functions and concluded that XIRR is more accurate because it takes into account the actual payment dates of the loan and thus allows us to calculate annualized interest rates even with irregular repayment schedules.

But for the more technical among us, I realize that even this may not be sufficient. Today I’m going to demonstrate how to write a computer program that is as accurate as Excel 2007’s XIRR function. This article is likely to be of less broad interest, but it provides transparency into how we will calculate interest rates for future data collection trips; and it may be useful for MFIs that wish to automate interest rate calculations for a larger data set than can be handled with Excel.

Let’s start with the EIR formula and describe two techniques.

  • EIR = cf*(1+rate)^n

cf = cashflow, n=number of periods/year

Simple Guess and Check

The first technique is to make a guess about the interest rate and then run the numbers through the EIR formula to see how close you are. You then iterate, guessing somewhere in the middle of your previous guesses, or widening your area by doubling. The advantage of this technique is that it is simple and it gets you the right answer eventually (or at least fairly accurately given enough guesses).

Newton’s method

A more advanced way to solve the EIR formula is to use Calculus. It’s still a “guessing” technique, but it is much more efficient and elegant.

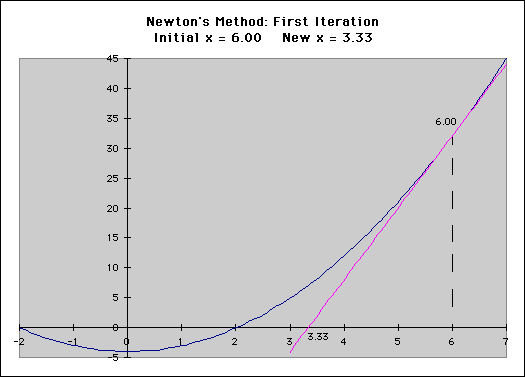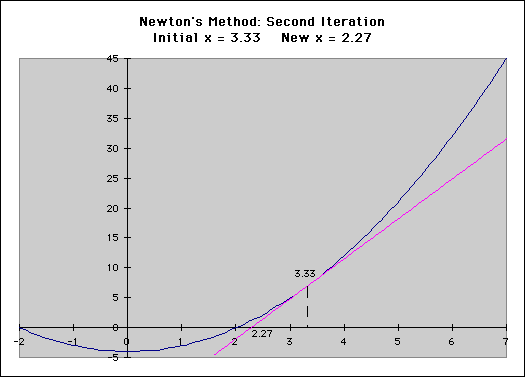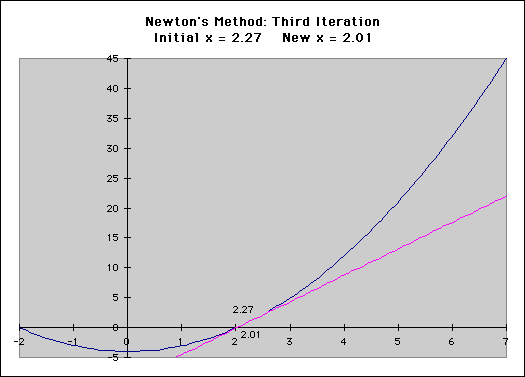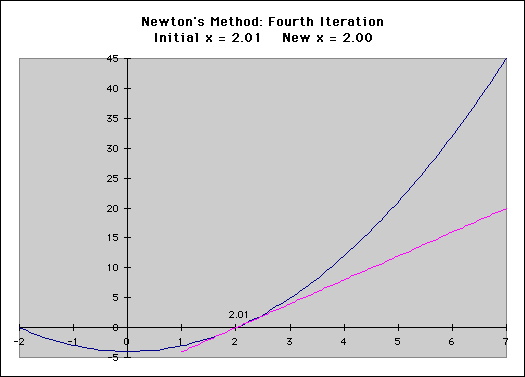
It’s easier to visualize this technique if we draw a graph and plot an initial guess, with the goal of finding the point on the graph where it crosses the x axis.

We start by making an initial guess and then figuring out what the “tangent” line at that point would be. This is the same thing as the derivative of the EIR calculation:

  • EIR = cf*(1+rate)^n
  • f’rate = cf*n*(rate+1)^(n-1) = pink tangent line is the derivative

cf = cashflow, n=number of periods/year

We can then figure out where the tangent line intersects the x axis and use that to make a much more accurate second guess.

The speed advantage the Newton-Raphson method has over a simple guess and check technique is quite remarkable. It is common to be able to achieve a result that matches Excel to within 8 decimal places in 5-10 iterations.

Implementing Newton-Raphson

Fortunately for me, I didn’t have to implement the entire Newton-Raphson algorithm myself because the programming language I use already has a library to do this. I just give it the EIR function and the derivative function and it does the rest.

For the programmers out there, here are a few links to implementations in various languages:

  • C#: uses bisection rather than Newton’s method
  • Java
  • Python

Related Information:

For those of you who would like to know more, please explore the following links:

Next Article:

Calculating Effective Interest Rates Using Cashflow Discounting

by

Here’s a post I wrote for Microfinance Transparency on October 26, 2010:

(Note: not all formatting carried over from the MFT Blog)

In a previous post, I described the technique that computer programs like Microsoft Excel use to calculate the XIRR (effective interest rate) as a very smart version of “guess and check.” The post on Newton’s Method described how the “guessing” part works, but it did not describe how the computer is able to finally verify when it has the correct EIR figure — the “check” part.

In today’s post, I’m going to describe the process that a computer program uses to generate a discounted cashflow, a method of calculating the value of a cashflow that uses the time-value of money. By adding up the discounted cashflows we are able to determine whether we have the correct EIR.

I’m going to start with a sample loan of $4,825.00 that was disbursed on the 28th of the month but is paid back on the 16th of the month every month for about a year. The fact that the disbursement date is not exactly one month prior to the first repayment means that a simple IRR formula can not be used for accurate results, and the calculation must take all the actual dates into account. The exact details are at right.

How to Check an EIR

The first step in the process is to come up with a guess. For my example, I’ll start with a guess of 30 percent. The next step is then to take that 30% rate and plug it into the discounting formula for each date of the loan:

Discounted cashflow = cashflow * (rate +1)^(-days/365)

This gives us the discounted value of the cashflow for each date period. We then add up all the discounted cashflows to produce a total. This total should be 0 if the rate is correct, indicating that discounted cashflow is equivalent to the nominal cashflow at the specified rate. If it is not 0, we guess again, until we get closer and closer to 0. (For our purposes we decided that 8 decimal places of accuracy is good enough!) Below, you will see that Newton’s method is able to guess the correct EIR in only 5 guesses! [Read more…]

How to Bring Neighbors Together with a Block Party

by

3rd Street Block Party, 2022

Lessons from our Street’s first Block Party in Decades

I’ve been wanting to hold a block party on my street to help neighbors get to know each other and build community spirit.  This post details how our street held our first block party in decades.  My hope is that other streets will learn from this on how to  hold their own block parties.

Walking the Neighborhood

I’ve being going on regular walks around Akron for over a decade and after a day spent working from home, I often feel like getting some social time.  While on my walks, if a resident seems open to talking I’ll often strike up a conversation.

When I’m on my own street and I see a neighbor, I test their receptivity  and mention the idea of the block party.  If I haven’t talked with them before I point out where I live on the street so they can tell that I’m one of their neighbors and this block party thing is “legit”.

We were able to get 49 attendees to the party, which is quite a high percentage of the neighborhood.

3rd Street Block Party, 2022

Talking to people in person

I talked with everyone on the street at least 2-3 times.  I don’t think I would have gotten the response I did without the personal touch.  I also got ideas from people on how to make the idea work.  I had the basic concept, but I didn’t have a location or date at the beginning.  The date and location came later after I spoke with people. [Read more…]

How an Engineering Student’s Question Prevented a NYC Skyscraper from Falling Down

by

Citigroup Center

Engineering crisis of 1978 (from Wikipedia)

Due to material changes during construction, the building as initially completed was structurally unsound. William LeMessurier‘s original design for the chevron load braces used welded joints. To save money, Bethlehem Steel changed the plans in 1974 to use bolted joints, which was accepted by LeMessurier’s office but not known to the engineer himself.[22] Furthermore, according to The New Yorker, LeMessurier originally only needed to calculate wind loads from perpendicular winds under the building code; in typical buildings, loads from quartering winds at the corners would be less.[22][159] In June 1978, after an inquiry from Princeton University engineering student Diane Hartley, LeMessurier recalculated the wind loads on the building with quartering winds.[159][f] He found that, for four of the eight tiers of chevrons, such winds would create a 40 percent increase in wind loads and a 160 percent increase in load at the bolted joints.[22]

Citicorp Center’s use of bolted joints and the increased loads from quartering winds would not have caused concern if these issues had been isolated from each other. However, the combination of the two findings prompted LeMessurier to run tests on the structural safety.[103] The original welded-joint design could withstand the load from straight-on and quartering winds, but a 75-mile-per-hour (121 km/h) hurricane force quartering wind would exceed the strength of the bolted-joint chevrons.[99] With the tuned mass damper active, LeMessurier estimated that a wind capable of toppling the building would occur on average once every 55 years.[162][161] If the tuned mass damper could not function due to a power outage, a wind strong enough to cause the building’s collapse would occur once every 16 years on average.[162] LeMessurier also discovered that his firm had used New York City’s truss safety factor of 1:1 instead of the column safety factor of 1:2.[99] [Read more…]