Here’s an article I wrote for Microfinance Transparency in February 24, 2010:
Chuck Waterfield and Alexandra Fiorillo, MFTransparency’s CEO and VP respectively, have been doing many presentations about how interest rates can be calculated using our excel tool, but we haven’t yet featured a story on our blog about our data collection process and our corresponding excel tool. Although technical, interest rate calculations are really at the heart of MFTransparency’s mission and calculating accurate interest rates is vital to providing transparent pricing data. So today, I would like to give you a brief demonstration of the IRR and XIRR Excel functions, as a way to provide background for the techniques we’ve used to automate interest rate calculations on our website.
For those of you less familiar with excel, this spreadsheet software offers numerous formulas allowing quick and easy calculations within each spreadsheet. As it is particularly geared towards financial use, there are ready-made formulas specifically meant for calculating interest rates. The most basic (but still powerful) calculation is the internal rate of return.
IRR() : Internal Rate of Return
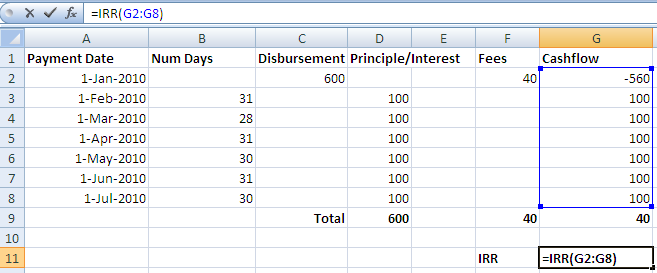
The internal rate of return formula is capable of taking a cash flow and returning the per-period interest rate. It assumes equal lengths of time between each amount in the cash flow. Let’s first start with a sample spreadsheet of loan payments, and use the IRR function to calculate the interest rate.
You can see that by applying the IRR formula, we get an “Internal Rate of Return” for the loan. This IRR can then be multiplied by the number of periods in a year to get the APR. Annual Percentage Rate is the standardized format most commonly used in the United States.
- APR = IRR * n, where n is the number of payments per year.
- 24.09% = 0.0200757 * 12
The EIR takes into account the effect of compound interest and can be calculated using the formula. This is the standardized interest rate often reported in European countries:
- EIR = ((1+IRR)^n) -1)
- 26.94% = ((1+ 0.0200757)^12)-1)
The IRR function is sufficient when there are equal (or near equal) periods between repayments, but what about when repayments occur irregularly? Prior to Excel 2007, there was no easy solution… but thankfully the wizards at microsoft have now provided us with a solution:
XIIR(): accounts for actual payment dates
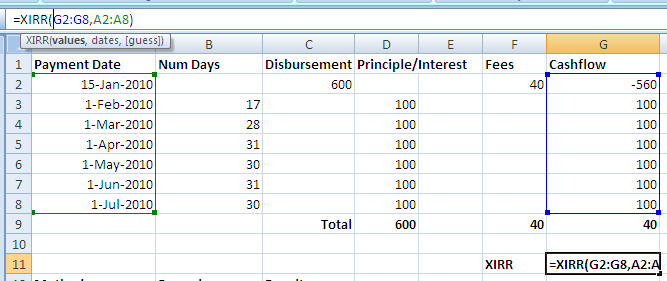
As mentioned above, the XIRR function is useful for loans with irregular repayment schedules, and is only available in newer versions of Excel (2007) and in recent versions of Open Office.
Notice that the XIRR function takes into account the payment dates in addition to the payment amounts. It actually provides us with the EIR (so annualized interest rate WITH compounding) for the cash flow in question. We won’t get into the math behind this, but suffice it to say that this formula is powerful, and a significant step up in allowing accurate calculations of interest rates. If you download the sample spreadsheet and play with the numbers, you can see the effect that an early first payment and a short month (February) have on the XIIR result.
- better EIR = Excel XIIR()
- XIRR() = 32.16%
So XIRR is a more accurate way to calculate the interest rate because it takes into account both actual payment dates and the effect of compound interest.
These tools are what allow MFTransparency to calculate accurate interest rates that are comparable between MFIs, despite different/irregular repayment schedules, additional fees, etc. So while they may seem mundane, they are actually the crux of transparent pricing!
In a future post, I’ll explain how software programmers can efficiently add advanced Excel 2007-like XIRR calculations to their software programs.
Further Information
For those of you who would like to know more about interest rate calculation, I encourage you to check out the following:
- Example Spreadsheet: examples from this blog entry
- Effective Interest Rate, by William Tucker (pdf)
The next post in this series, “Calculating Interest Rates Using Newton’s Method” is a more advanced version of this article that explains the algorithm behind the XIIR formula, and how this technique can be applied in programming languages like C#, python, or Java.
P.S. For investors, Excel’s XIRR feature can also be used to calculate a Personal Investment Rate of Return, which is more relevant than the values that appear in a fund’s prospectus because it takes into account the investor’s actual purchase history.
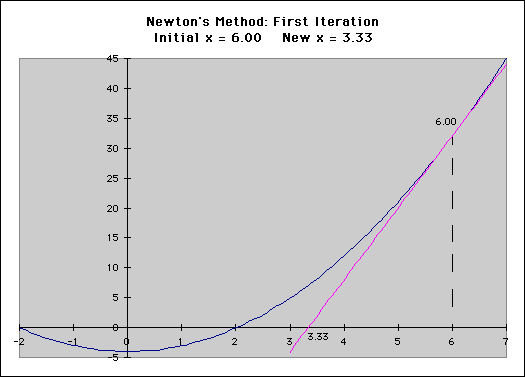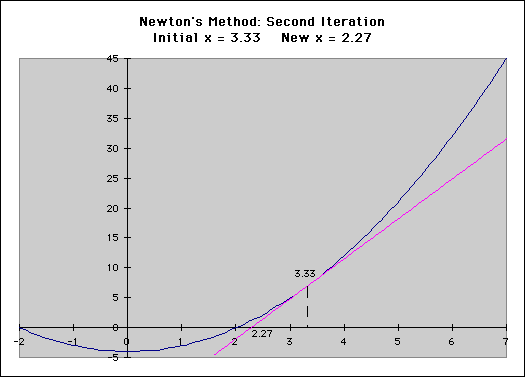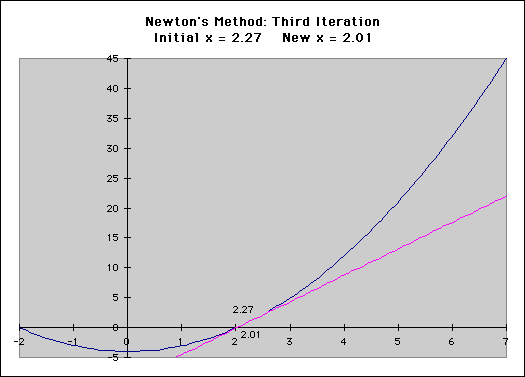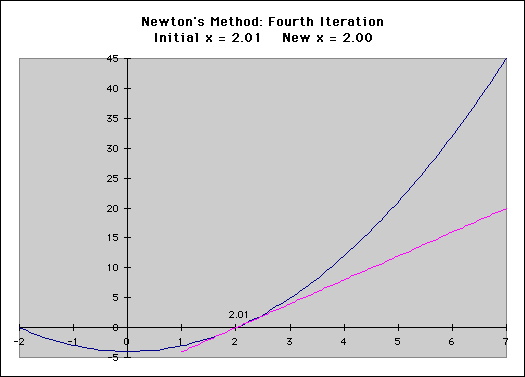
 In a previous post, I described the technique that computer programs like Microsoft Excel use to calculate the
In a previous post, I described the technique that computer programs like Microsoft Excel use to calculate the 